@Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting

[[Abstract]]

• Many real-world applications require the prediction of long sequence time-series, such as electricity consumption planning. Long sequence time-series forecasting (LSTF) demands a high prediction capacity of the model, which is the ability to capture precise long-range dependency coupling between output and input efficiently. Recent studies have shown the potential of Transformer to increase the prediction capacity. However, there are several severe issues with Transformer that prevent it from being directly applicable to LSTF, including quadratic time complexity, high memory usage, and inherent limitation of the encoder-decoder architecture. To address these issues, we design an efficient transformer-based model for LSTF, named Informer, with three distinctive characteristics: (i) a ProbSparse self-attention mechanism, which achieves O(L log L) in time complexity and memory usage, and has comparable performance on sequences’ dependency alignment. (ii) the self-attention distilling highlights dominating attention by halving cascading layer input, and efficiently handles extreme long input sequences. (iii) the generative style decoder, while conceptually simple, predicts the long time-series sequences at one forward operation rather than a step-by-step way, which drastically improves the inference speed of long-sequence predictions. Extensive experiments on four large-scale datasets demonstrate that Informer significantly outperforms existing methods and provides a new solution to the LSTF problem.

[[Attachments]]

• Informer_2021_Zhou.pdf

Long sequence [[Time Series Forecasting]] (LSTF)

• 长序列时间序列预测需要模型能够有效捕捉输出和输入之间精确的 long-range dependency coupling

LSTF 中使用 [[Transformer]] 需要解决的问题 #card #incremental

• self-attention 计算复杂度 $O(L^2)$

• 多层 encoder/decoder 结构内存增长

• dynamic decoding 方式预测耗时长

网络结构

ProbSparse self-attention

• 替换 inner product self-attention

  • [[Sparse Transformer]] 结合行输入和列输出

  • [[LogSparse Transformer]] cyclical pattern

  • [[Reformer]] locally-sensitive hashing(LSH) self-attention

  • [[Linformer]]

  • [[Transformer-XL]] [[Compressive Transformer]] use auxiliary hidden states to capture long-range dependency

  • [[Longformer]]

• 其他优化 self-attention 工作存在的问题

  • 缺少理论分析

  • 对于 multi-head self-attention 每个 head 都采用相同的优化策略

• self-attention 点积结果服从 long tail distribution

  • 较少点积对贡献绝大部分的注意力得分

  • 现实含义：序列中某个元素一般只会和少数几个元素具有较高的相似性/关联性

• 第 i 个 query 用 $q_i$ 表示

  • $\mathcal{A}\left(q_i, K, V\right)=\sum_j \frac{f\left(q_i, k_j\right)}{\sum_l f\left(q_i, k_l\right)} v_j=\mathbb{E}_{p\left(k_j \mid q_i\right)}\left[v_j\right]$

  • $p\left(k_j \mid q_i\right)=\frac{k\left(q_i, k_j\right)}{\sum_l f\left(q_i, k_l\right)}$

  • $k\left(q_i, k_j\right)=\exp \left(\frac{q_i k_j^T}{\sqrt{d}}\right)$

• query 稀疏性判断方法

  • $p(k_j|q_j)$ 和[[均匀分布]] q 的 [[KL Divergence]]

    • q 是均分分布，相等于每个 key 的概率都是 $\frac{1}{L}$

    • 如果 query 得到的分布类似于均匀分布，每个概率值都趋近于 $\frac{1}{L}$，值很小，这样的 query 不会提供什么价值。

    • p 和 q 分布差异越大的结果越是我们需要的 query

    • p 和 q 的顺序和论文中的不同 $D(p \| q)=\sum_{x} p(x) \log \frac{p(x)}{q(x)}=E_{p(x)}\left(\log \frac{p(x)}{q(x)}\right)$

  • $K L(q \| p)=\ln \sum_{l=1}^{L_k} e^{q_i k_l^T / \sqrt{d}}-\frac{1}{L_k} \sum_{j=1}^L q_i k_j^T / \sqrt{d}-\ln L_k$

    • 把公式代入，然后化解

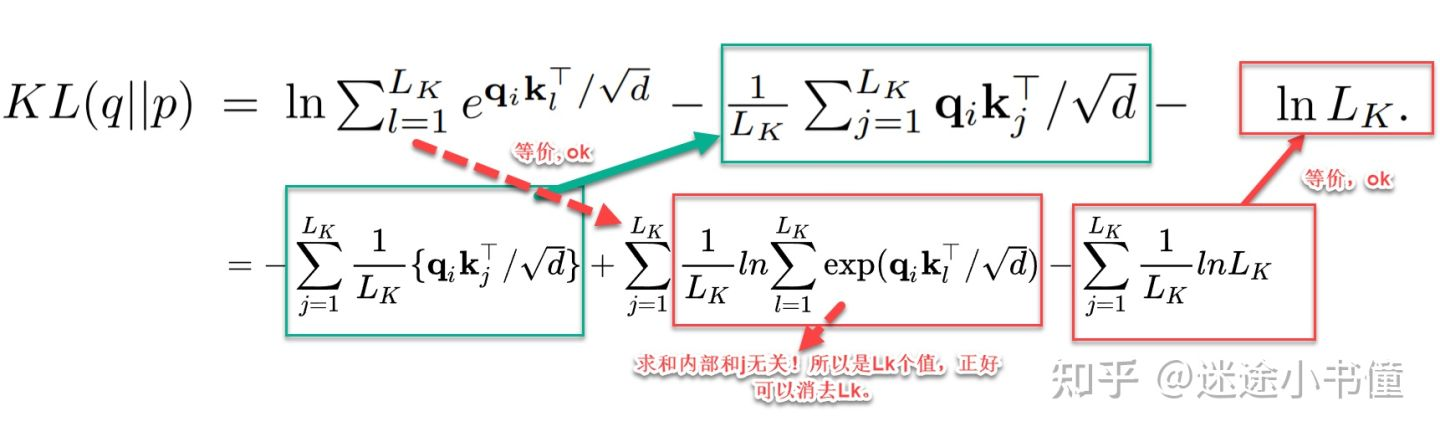
+ $M\left(q_i, K\right)=\ln \sum_{l=1}^{L_k} e^{q_i k_l^T / \sqrt{d}}-\frac{1}{L_k} \sum_{j=1}^{L_k} q_i k_j^T / \sqrt{d}$

  + 第一项是经典难题 log-sum-exp(LSE) 问题

  + 稀疏性度量 $M\left(q_i, K\right)$

    + $\ln L \leq M\left(q_i, K\right) \leq \max _j\left\{\frac{q_i k_j^T}{\sqrt{d}}\right\}-\frac{1}{L} \sum_{j=1}^L\left\{\frac{q_i k_j^T}{\sqrt{d}}\right\}+\ln L$

    + LSE 项用最大值来替代，即用和当前 qi 最近的 kj，所以才有下面取 top N 操作

      + $\bar{M}\left(\mathbf{q}_i, \mathbf{K}\right)=\max _j\left\{\frac{\mathbf{q}_i \mathbf{k}_j^{\top}}{\sqrt{d}}\right\}-\frac{1}{L_K} \sum_{j=1}^{L_K} \frac{\mathbf{q}_i \mathbf{k}_j^{\top}}{\sqrt{d}}$

+ $\mathcal{A}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{Softmax}\left(\frac{\overline{\mathbf{Q}} \mathbf{K}^{\top}}{\sqrt{d}}\right) \mathbf{V}$

  + $\bar{Q}$ 是稀疏矩阵，前 u 个有值

+ 具体流程

  + 为每个 query 都随机采样 N 个 key，默认值是 5lnL

    + 利用点积结果服从长尾分布的假设，计算每个  query 稀疏性得分时，只需要和采样出的部分 key 计算

  + 计算每个 query 的稀疏性得分

  + 选择稀疏性分数最高的 N 个 query，N 默认值是 5lnL

  + 只计算 N 个 query 和所有 key 的点积结果，进而得到 attention 结果

  + 其余 L-N 个 query 不计算，直接将 self-attention 层输入取均值(mean(V))作为输出

    + 除了选中的 N 个query index 对应位置上的输出不同，其他 L-N 个 embedding 都是相同的。所以新的结果存在一部分冗余信息，也是下一步可以使用 maxpooling 的原因

    + 保证每个 ProbSparse self-attention 层的输入和输出序列长度都是 L

+ 将时间和空间复杂度降为 $$O(L_K \log L_Q)$$

+ 如何解决 对于 multi-head self-attention 每个 head 都采用相同的优化策略

现象？

  + 每个 query 随机采样 key 这一步每个 head 的采样结果是相同的

  + 每一层 self-attention 都会先对 QKV 做线性转换，序列中同一个位置不同 head 对应的 query、key 向量不同

  + 最终每个 head 中得到的 N 个稀疏性最高的 query 也是不同的，相当于每个 head 都采取不同的优化策略

Self-attention distilling

• 突出 dominating score，缩短每一层输入的长度，降低空间复杂度到 $\mathcal{O}((2-\epsilon) L \log L)$

• encoder 层数加深，序列中每个位置的输出已经包含序列中其他元素的信息，所以可以缩短输入序列的长度

  • 过 attention 层后，大部分位置值相同

• 激活函数 [[ELU]]

• 通过 Conv1d + max-pooling layer 缩短序列长度

class ConvLayer(nn.Module):
    def __init__(self, c_in):
        super(ConvLayer, self).__init__()
        self.downConv = nn.Conv1d(in_channels=c_in,
                                  out_channels=c_in,
                                  kernel_size=3,
                                  padding=2,
                                  padding_mode='circular')
        self.norm = nn.BatchNorm1d(c_in)
        self.activation = nn.ELU()
        self.maxPool = nn.MaxPool1d(kernel_size=3, stride=2, padding=1)

    def forward(self, x):
        x = self.downConv(x.permute(0, 2, 1))
        x = self.norm(x)
        x = self.activation(x)
        x = self.maxPool(x)
        x = x.transpose(1,2)
        return x

Generative style decoder

• 预测阶段通过一次前向得到全部预测结果，避免 dynamic decoding

• 不论训练还是预测，Decoder 的输入序列分成两部分 $X_{feed dcoder} = concat(X_{token}, X_{placeholder})$

  • 预测时间点前一段已知序列作为 start token

  • 待预测序列的 placeholder 序列

• 经过 deocder 后，每个 placeholder 都有一个向量，然后输入到一个全链接层得到预测结果

• 为什么用 generative style decoder #card

  • 解码器能捕捉任意位置输出和长序列依赖关系

  • 避免累积误差

Experiment

• Baseline

  • [[ARIMA]] [[Prophet]] [[DeepAR]]

  • [[Reformer]] dynamic decoding

• 实验设计

  • Univariate Time-series Forecasting

  • Multivariate Time-series Forecasting

    • LSTnet 是基线模型

  • Ablation Study

Input representation

• 提供时序信息

• 不是天级别更新的模型需要 global time stamp

  • week，month，holiday embedding

• 额外实验

  • 利用 t0-t1 的特征预测 t2-t3 结果还不错

  • 可能是 local time stamp 和 global time stamp 让 informer 不依赖自回归结果还能有不错的预测结果

See Also

• [[Informer/Code]]

• [[Informer/Question]]

Ref

• Informer: 一个基于Transformer的效率优化的长时间序列预测模型 - 知乎 (zhihu.com)